The English encyclopedia Allmultimedia.org will be launched in two phases.
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
The final launch of the Allmultimedia.org will take place on February 27, 2026
(shortly after the 2026 Winter Olympics).
Mocninná funkce
Z Multimediaexpo.cz
(Rozdíly mezi verzemi)
(+ Nový článek) |
m (Nahrazení textu „<math>“ textem „<big>\(“) |
||
| Řádka 1: | Řádka 1: | ||
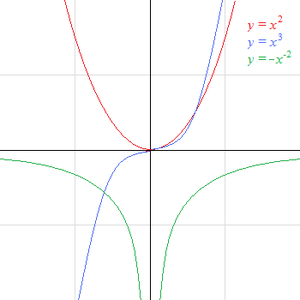
[[Soubor:Funkcie mocniny2.png|thumb|300px|Grafy mocninných funkcí pro exponent 2, 3 a -2]] | [[Soubor:Funkcie mocniny2.png|thumb|300px|Grafy mocninných funkcí pro exponent 2, 3 a -2]] | ||
'''Mocninná funkce''' je [[Elementární funkce|elementární matematická funkce]] tvaru | '''Mocninná funkce''' je [[Elementární funkce|elementární matematická funkce]] tvaru | ||
| - | :< | + | :<big>\(f\colon x \mapsto a x^r \qquad a,r \in \mathbb{R},</math> |
| - | kde < | + | kde <big>\(a</math> a <big>\(r</math> jsou [[konstanta|konstanty]] a <big>\(x</math> je proměnná. |
== Definiční obor == | == Definiční obor == | ||
| - | Definiční obor závisí na exponentu < | + | Definiční obor závisí na exponentu <big>\(r</math>. |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| - | ! !! < | + | ! !! <big>\(r > 0</math> !! <big>\(r < 0</math> |
|- | |- | ||
| - | | < | + | | <big>\(r \in \mathbb{Z}</math> || style="text-align:center" | <big>\(\mathbb{R}</math> || style="text-align:center" | <big>\(\mathbb{R}\setminus\{0\}</math> |
|- | |- | ||
| - | | < | + | | <big>\(r \notin \mathbb{Z}</math> || style="text-align:center" | <big>\(\mathbb{R}^+_0</math> || style="text-align:center" | <big>\(\mathbb{R}^+</math> |
|} | |} | ||
== Obor hodnot == | == Obor hodnot == | ||
| - | Obor hodnot závisí na konstantě < | + | Obor hodnot závisí na konstantě <big>\(a</math> a exponentu <big>\(r</math>. |
{| class="wikitable" | {| class="wikitable" | ||
| - | ! || colspan="2" | < | + | ! || colspan="2" | <big>\(r > 0</math> || colspan="2" | <big>\(r < 0</math> |
|- | |- | ||
| - | ! !! < | + | ! !! <big>\(r</math> sudé <br /> nebo <big>\(\notin \mathbb{Z}</math> !! <big>\(r</math> liché !! <big>\(r</math> sudé <br /> nebo <big>\(\notin \mathbb{Z}</math> !! <big>\(r</math> liché |
|- | |- | ||
| - | | < | + | | <big>\(a > 0</math> || style="text-align:center" | <big>\(\mathbb{R}^+_0</math> || style="text-align:center" | <big>\(\mathbb{R}</math> || style="text-align:center" | <big>\(\mathbb{R}^+</math> || style="text-align:center" | <big>\(\mathbb{R}\setminus\{0\}</math> |
|- | |- | ||
| - | | < | + | | <big>\(a < 0</math> || style="text-align:center" | <big>\(\mathbb{R}^-_0</math> || style="text-align:center" | <big>\(\mathbb{R}</math> || style="text-align:center" | <big>\(\mathbb{R}^-</math> || style="text-align:center" | <big>\(\mathbb{R}\setminus\{0\}</math> |
|} | |} | ||
Verze z 14. 8. 2022, 14:49
Mocninná funkce je elementární matematická funkce tvaru
- \(f\colon x \mapsto a x^r \qquad a,r \in \mathbb{R},</math>
kde \(a</math> a \(r</math> jsou konstanty a \(x</math> je proměnná.
Definiční obor
Definiční obor závisí na exponentu \(r</math>.
| \(r > 0</math> | \(r < 0</math> | |
|---|---|---|
| \(r \in \mathbb{Z}</math> | \(\mathbb{R}</math> | \(\mathbb{R}\setminus\{0\}</math> |
| \(r \notin \mathbb{Z}</math> | \(\mathbb{R}^+_0</math> | \(\mathbb{R}^+</math> |
Obor hodnot
Obor hodnot závisí na konstantě \(a</math> a exponentu \(r</math>.
| \(r > 0</math> | \(r < 0</math> | |||
|---|---|---|---|---|
| \(r</math> sudé nebo \(\notin \mathbb{Z}</math> | \(r</math> liché | \(r</math> sudé nebo \(\notin \mathbb{Z}</math> | \(r</math> liché | |
| \(a > 0</math> | \(\mathbb{R}^+_0</math> | \(\mathbb{R}</math> | \(\mathbb{R}^+</math> | \(\mathbb{R}\setminus\{0\}</math> |
| \(a < 0</math> | \(\mathbb{R}^-_0</math> | \(\mathbb{R}</math> | \(\mathbb{R}^-</math> | \(\mathbb{R}\setminus\{0\}</math> |
| Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010 |
|---|
| Informace o článku.
Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. |