Hillova sféra

Z Multimediaexpo.cz

(Rozdíly mezi verzemi)

Aktuální verze z 14. 8. 2022, 14:52

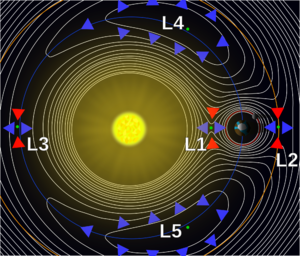
Znázornění Lagrangeových bodů pro planetu, kolem níž obíhá jeden měsíc. Body L1 a L2 leží na hranici Hillovy sféry.

Hillova sféra je oblast kolem nějakého tělesa (planety, měsíce), v níž má toto těleso silnější gravitační vliv než jiné masivnější těleso, kolem kterého obíhá. V případě planety je to např. oblast, v které má větší gravitační vliv, než hvězda, kolem které obíhá. V této oblasti musí ležet celá oběžná dráha jejího měsíce, jinak by tento měsíc planeta časem ztratila. Hillova sféra má přibližně sférický tvar a Lagrangeovy body L1 a L2 jsou dva hraniční body této oblasti. Hillovu sféru definoval americký astronom George William Hill na základě práce francouzského astronoma Edouarda Rocheho.

Pro Zemi má Hillova sféra poloměr 1,5 mil. km.^[1]

Vztah pro výpočet poloměru Hillovy sféry

Pokud je hmotnost menšího tělesa (např. planety Země) m a obíhá kolem hmotnějšího tělesa (např. v případě Země kolem Slunce), které má hmotnost M po eliptické dráze s hlavní poloosou a a excentricitou e, potom je poloměr r Hillovy sféry toto menší těleso přibližně:^[2]

\(r \approx a (1-e) \sqrt[3]{\frac{m}{3 M}}\)

Pokud se tvar oběžné dráhy menšího tělesa (planety) blíží tvaru kružnice, je hodnota excentricity velmi malá a můžeme ji zanedbat. Pak lze poloměr Hillovy sféry určit ze vztahu:

\(r \approx a \sqrt[3]{\frac{m}{3M}}\)

V případě planety Země platí tyto údaje: m = 5,97×10²⁴ kg, M = 1,99×10³⁰ kg, a = 149,6 millionů km = 149,6×10⁹ m. Hodnota Hillovy sféry pro Zemi tedy vychází kolem 1,5 millionu km (0,01 AU). Oběžná dráha Měsíce má poloměr 0,384 400 milionu km a pohodlně se tedy vejde do spočtené hodnoty poloměru Hillovy sféry pro Zemi. Nehrozí tedy nebezpečí, že by Měsíc mohl být odtržen od Země a nezávisle mohl začít obíhat kolem Slunce.

Reference

Související články

Rocheova sféra

Náklady na energie a provoz naší encyklopedie prudce vzrostly. Potřebujeme vaši podporu... Kolik ?? To je na Vás. Náš FIO účet — 2500575897 / 2010
Informace o článku. Článek je převzat z Wikipedie, otevřené encyklopedie, do které přispívají dobrovolníci z celého světa. Tento text je dostupný za podmínek Creative Commons 3.0 Unported – creativecommons.org. Originální článek na české Wikipedii

[0] PLANETKY PRO POZOROVATELE

[HamiltonBurns92-1] Orbital stability zones about asteroids. II - The destabilizing effects of eccentric orbits and of solar radiation

[1]

[2]

@@ Řádka 7: / Řádka 7: @@
 Pokud je hmotnost menšího tělesa (např. planety Země) ''m'' a obíhá kolem hmotnějšího tělesa (např. v případě [[Země]] kolem [[Slunce]]), které má hmotnost ''M'' po [[elipsa|eliptické]] dráze s [[hlavní poloosa|hlavní poloosou]] ''a'' a [[excentricita|excentricitou]] ''e'', potom je poloměr ''r'' Hillovy sféry toto menší těleso přibližně:<ref name="HamiltonBurns92">[http://adsabs.harvard.edu/cgi-bin/nph-bib_query?bibcode=1992Icar...96...43H&amp;db_key=AST&amp;data_type=HTML&amp;format=&amp;high=444b66a47d16486 Orbital stability zones about asteroids. II - The destabilizing effects of eccentric orbits and of solar radiation]</ref>
-:<big>\(r \approx a (1-e) \sqrt[3]{\frac{m}{3 M}}</math>
+:<big>\(r \approx a (1-e) \sqrt[3]{\frac{m}{3 M}}\)</big>
 Pokud se tvar oběžné dráhy menšího tělesa (planety) blíží tvaru [[kružnice]], je hodnota excentricity velmi malá a můžeme ji zanedbat. Pak lze poloměr Hillovy sféry určit ze vztahu:
-:<big>\(r \approx a \sqrt[3]{\frac{m}{3M}}</math>
+:<big>\(r \approx a \sqrt[3]{\frac{m}{3M}}\)</big>
 V případě planety Země platí tyto údaje: ''m'' = 5,97×10<sup>24</sup> kg, ''M'' = 1,99×10<sup>30</sup> kg, ''a'' =  149,6 millionů km = 149,6×10<sup>9</sup> m. Hodnota Hillovy sféry pro Zemi tedy vychází kolem 1,5 millionu km (0,01 AU).  Oběžná dráha Měsíce má poloměr 0,384 400 milionu km a pohodlně se tedy vejde do spočtené hodnoty poloměru Hillovy sféry pro Zemi. Nehrozí tedy nebezpečí, že by Měsíc mohl být odtržen od Země a nezávisle mohl začít obíhat kolem Slunce.